Tarrasch V3.13a

This is quite an important new release. Although I was initially pretty happy with Tarrasch V3.12a released some 18 months ago, inevitably bugs and issues emerged as I used it as a workhorse for all my chess work. Some of the problems were embarrassing I am sad to admit. In the last few months I have worked quite hard on resolving the problems and refining Tarrasch (anyone who doubts me is welcome to consult the Github log).

I issued a minor update Tarrasch V3.12b a couple of months ago, and now this more significant upgrade which I hope is a significant milestone. Details of the fixes and refinements can be found on Github and on the project news page.

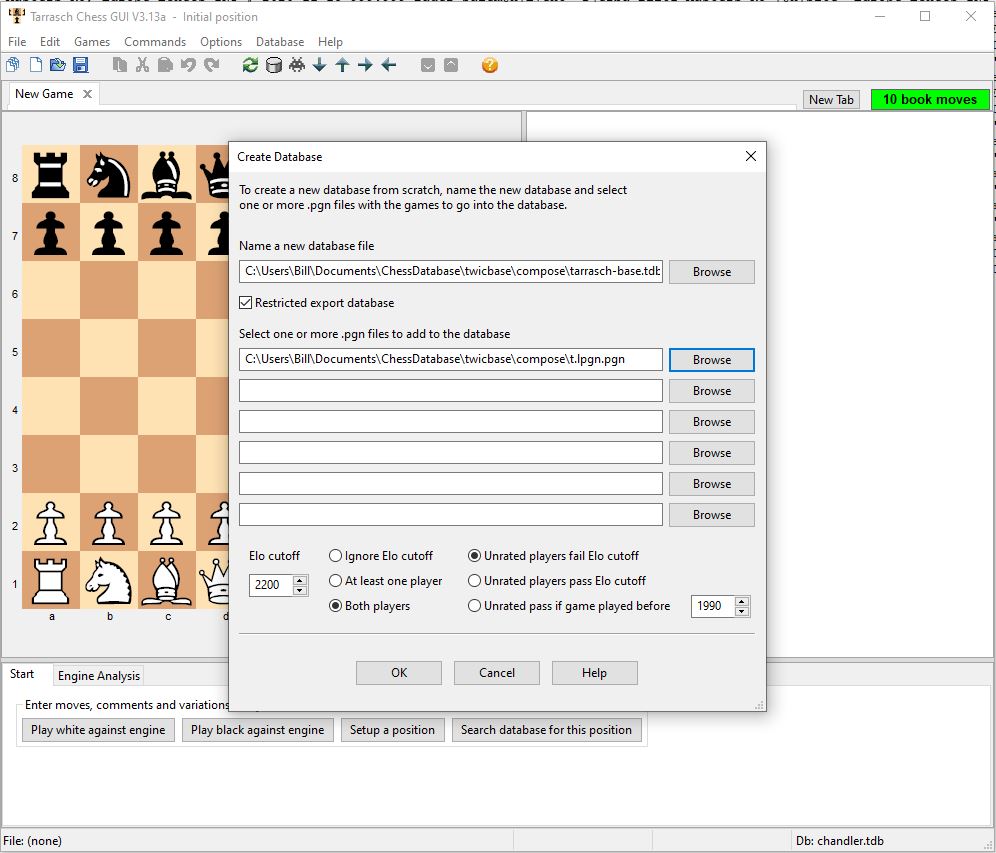
A very significant change is the new TarraschBase games database which replaces Kingbase Lite as the default Tarrasch database. Pierre Havard’s Kingbase project has been abandoned, so it was necessary to move on, and I think the solution found is a big win for Tarrasch. I am indebted to Mark Crowther, the dynamo behind the awesome TWIC (The Week In Chess) project, who has given me permission to use TWIC as the basis of the new TarraschBase database. TarraschBase comprises all TWIC games since 1995 played by two 2200+ players (similar criteria to Kingbase Lite), excluding some blitz and bullet events. My intention is to add a few hundred thousand pre 1995 (i.e. pre TWIC) games to make TarraschBase a universal solution for the casual chess fan. I will do that when (if) I get explicit permission from someone who owns an existing database to source the games from.

To protect Mark’s commercial interests we have agreed that the TWIC games should be kept within the Tarrasch program as much as possible. To this end I have made TarraschBase a “restricted” database, which means that no more than 10,000 games at a time can be exported out to PGN format. I feel that this is a very reasonable and it doesn’t affect any of Tarrasch’s usual features.

Of course if you want unrestricted access to all the TWIC games you can buy Mark’s complete TWIC database directly from him, it’s good value and I encourage you to do that.

I’d like to quickly document here how I currently put TarraschBase together. This might be of interest to someone who wrangles PGN files. Here is a version of the Windows/DOS batch file I made to capture the process;

REM prepare tarrasch-base 17 Nov 2020, remember to use .CBH
REM versions of individual twic files, then use ChessBase
REM to convert to .pgn (for name convention compatibility to
REM twic-1-to-1346.pgn which was itself converted from .CBH by
REM ChessBase)
echo twic1347.pgn>twic.lst
echo twic1348.pgn>>twic.lst
echo twic1349.pgn>>twic.lst
echo twic1350.pgn>>twic.lst
echo twic1351.pgn>>twic.lst
echo twic1352.pgn>>twic.lst
echo twic1353.pgn>>twic.lst
echo twic1354.pgn>>twic.lst
echo twic1355.pgn>>twic.lst
echo twic1356.pgn>>twic.lst
echo twic1357.pgn>>twic.lst
echo twic1358.pgn>>twic.lst
echo twic-1-to-1346.pgn>>twic.lst
pgn2line -p -r -l twic.lst twic-1-to-1358.lpgn
del twic-1-to-1358.pgn
ren twic-1-to-1358.lpgn.pgn twic-1-to-1358.pgn
tournaments -b twic-1-to-1358.lpgn tournaments-1-to-1358.txt
wordsearch -i blitz tournaments-1-to-1358.txt >black-list.txt
wordsearch -i bullet tournaments-1-to-1358.txt >>black-list.txt
wordsearch -i 5' tournaments-1-to-1358.txt >>black-list.txt
pgn2line -p -n +y 1995 -b black-list2.txt twic-1-to-1358.pgn t.lpgn
REM final pgn is in t.lpgn.pgn

I obtained the TWIC database through TWIC 1346 from Mark a few weeks back, and have added TWIC 1347 through 1358 since. I processed the combination of one huge PGN and 12 small PGNs with my own pgn2line.exe utility. I have been working on pgn2line.exe off and on for a while now, and I think it captures an excellent approach to managing collections of PGN files. It is much easier to wrangle chess games in a text format related to PGN, but with the feature that each game is on one line. (Admittedly the lines are rather long!). You can check out the details on the pgn2line Github page. The pgn2line program is very good at taking a big (or small) collection of PGN files, sorting and deduplicating all the games from the entire collection and putting it all back together in one optimally sorted (as far as this is possible) file. It supports various transformations on the Event/Site information for each game, including white lists, black lists and fixups (renames). Player name reports are supported, and players names can also be fixed up.

In the batch file above pgn2line creates a PGN file in reverse order (most recent first) to suit Tarrasch, with games from prior to 1995 and Events that include the magic words Blitz and Bullet removed. The ancillary programs tournaments and wordsearch are included in the pgn2line release on Github. The final step of excluding games involving players less than 2200 takes place in Tarrasch itself.

Sargon 1978

In an ideal world I would have been using the Covid-19 lockdown to improve and refine Tarrasch. Unfortunately it’s far from an ideal world, and instead of that I’ve been porting the ancient chess program Sargon (1978 version!) so it can run on modern machines.

I have put a lot (frankly a ridiculous amount) of effort into the project. But I’ve finally finished, and if you are interested in retro computing and would like to play Sargon 1978 on Tarrasch, you can check out the whole project on the project Github page.

Tarrasch V3.12a

I have entered a kind of “pruning the roses” phase of Tarrasch maintenance. By this I mean I am pretty happy with Tarrasch, I am not planning massive changes, but I will continue to tweak and refine as limitations and flaws catch my notice and irritate me sufficiently to spark action.

In the last couple of days I’ve put out a release that fits with this theme. The new V3.12a release fixes one interoperability issue with other chess programs, and refines a couple of behaviours that have arisen since the fairly significant V3.10a update.

SInce V3.10a, Tarrasch responds to Windows Explorer requests to open a new file more sanely in the case that Tarrasch is already running. Previously, it would start a new instance of Tarrasch (not good). Now it loads the file in the existing instance of Tarrasch (good). A problem arises if the user is doing something that makes it inadvisable or wrong to just open the new file, for example browsing games in a game dialog (either a file, clipboard, database or session game dialog). I must admit that in the original V3.10a I didn’t check for this and just opened the file over the top. This seemed to work (ish) but wasn’t a proper solution. Later on I refined things and ignored such file open requests in those circumstances. With V3.12a I introduce what I hope is the ultimate refinement – Tarrasch waits for the user to finish what they are doing, then respectfully asks “Do you still want to open file x.pgn?”

Also since V3.10a, Tarrasch doesn’t completely cancel a file open if the user cancels the game dialog after opening a file. This policy is generally less confusing, you don’t have to pick a particular game when you open the file, you can cancel and you get the first game by default. But I’ve found that there is a tendency for Tarrasch to open too many tabs if you really just want to quickly look into a file this way without following on and doing anything with it. With V3.12a I detect that behaviour (opening file after file – cancelling the game dialog instead of selecting a game) and I don’t open a new tab for the new file if that’s what the user is doing.

The final significant change in V3.12a is that Tarrasch now handles a UTF-8 BOM at the start of PGN files (from other chess programs) without causing any issues. It still seems weird to me as an old school programmer that these days it is considered reasonable to start text files with 3 bytes of apparent binary gibberish, but “it is what it is” as the kids say. For the non-technical, this means that Tarrasch will be able to process files from programs like Chessbase without causing subtle downstream issues in the PGN files it creates (specifically orphaned header lines – Tarrasch itself copes with them okay, but not all chess programs do). You probably expected and deserved this to be the case before V3.12a, my apologies that this wasn’t always the case.

I have never blogged here about some quite large changes to Tarrasch since V3.03a which was a stable release for a year or so. Basically V3.10a brought some pretty significant changes, and the smaller changes since have largely been about smoothing off some rough edges that emerged.

The News page of triplehappy.com does cover all the recent changes pretty well. As I look through the itemised changes the following improvements jump out at me as being really significant;

• The games dialogs, so important to Tarrasch, are now much more usefully resizable, and the size and position of these dialogs persist across sessions. Apart from anything else this makes Tarrasch usable on a wider variety of machines.
• The Windows Explorer shell open file behaviour is dramatically improved, in particular since only a single instance of Tarrasch is now opened. It is now much more sensible to associate Tarrasch to the .pgn file type and in fact the installation program has been changed to make that option available.
• There are a couple of new status fields as the bottom of the screen, filling important holes. The db: field shows you which database you are using. The other new field shows draw counts. Both three fold repetition and 50 move rule counts will appear when it makes sense (and only then). You don’t have to ask for them.
• When you make a move by clicking on the destination square, the popup menu now has the “Cancel” option at the end instead of the default position at the beginning. This means if Tarrasch guesses right (it often does) you can make the move with just a long click, not a click-move-release.
• You can now select a Tarrasch database by opening it as a file – together with the db: status field, this will hopefully make using the database a lot more intuitive.

There’s also some bug fixes of course. One that particularly irks me is that in Tarrasch V3.03a the result of a Human-Engine game was not announced. How did I miss that? Actually I think I know, when I started Tarrasch the Engine v Human feature was front and centre of everything. Now that’s not the case, I am much more interested in Tarrasch as a general purpose chess workbench and tool for studying, working on, and documenting chess. I hardly ever use Engine v Human.

Unfortunately Tarrasch is still pretty much a niche program. The audience has not reached the critical threshold where large and embarrassing bugs like this are immediately noticed and reported. And since Tarrasch does include a lot of functionality, and is largely the work of one programmer who can’t realistically regression test everything on every release – there’s probably at least one embarrassing bug like this in every Tarrasch release. I wonder what’s hidden away somewhere in Tarrasch V3.12a? I don’t and can’t know for sure, and I’m not sure that ignorance really is bliss unfortunately.

 

Tarrasch V3.10c

I have been using Tarrasch V3.10 extensively since its release for my work on the New Zealand Chess Magazine. Yesterday I decided there was one issue I had encountered that required an immediate fix. In the cruel way these things often work out, a second such issue popped up today, less than 24 hours after publishing the previous fix. I decided to take a deep breath and just make another release. Sorry.

For the record – the problem fixed today appeared if you started a second instance of Tarrasch and then tried to use the database. Multiple instance Tarrasch is much improved with V3.10 – now when you use Windows explorer to load PGN files they will load into an instance of Tarrasch that’s already running rather than start a new instance. But you can start multiple Tarrasch instances if you want to. And helpfully if you do that, the second (and third etc.) instances won’t all load the database into memory. So multiple instances of Tarrasch don’t waste vast amounts of memory unnecessarily. But then if you do try to use the database you get a helpful message telling you how to force a database load. Sadly (so sadly) if you actually followed that advice Tarrasch would crash (a NULL pointer bug as it happens). This bug now fixed with Tarrasch V3.10c.

Tarrasch V3.10b

From my perspective the worst thing about providing a program to a substantial audience is managing the process of releasing new versions of the program to introduce new functionality and repair known flaws. I’d love to be able to guarantee that each new version was a monotonic improvement on previous versions, and it stresses me that I can’t make that guarantee. That’s one reason why until recently I left Tarrasch unchanged for 18 months, it was just less stressful that way.

As you no doubt realise, this is just a long winded way of saying I’ve pushed out an updated version today to address a very annoying problem that meant that V3.10a was not a monotonic improvement in all respects over the earlier release V3.03a.

Sometimes (often?) after a database search Windows was stealing the focus from Tarrasch and giving it to another program (often Chrome). Possibly this was an undesirable artifact from the improved resizability of the database window. Fixing this involved changing one line of code. Tarrasch now (re)asserts focus after a database search. That’s all I’ve changed for now, although I have ideas and plans that I want to release sooner rather than later.

My apologies to anyone affected by this problem, and for the necessity of this release.

On another topic, I actually owe Tarrasch users a more elaborate description of recent improvements than the brief outline that appears in the “News” section of the triplehappy.com website. That website needs some updates as well to reflect the new improvements. Sadly I am just too busy at the moment to provide either of these things. I’ll get to it soon, I promise.

Tarrasch V3.10a

Today I released Tarrasch V3.10a, the first release for well over a year. This release includes many refinements, bug fixes, and some important usability enhancements. You can see a full list of the changes on the News Page of triplehappy.com.

Clearly my development process needs further refinement, I have gone far too long between releases because many enhancements have been sitting on my development PC when they should have been out in the field.

I think I will try to roll out changes in smaller batches, more frequently in future. It’s been a long day, I think I will leave it at that for now.

Kingbase Update

It’s a little embarrassing that I haven’t posted anything in over a year, and that the last post is titled “Tarrasch V3.02”. When you’re steadily releasing minor updates you never know when you’re at a point that will prove to be relatively stable. I had some problems when I finally released Tarrasch V3 last year, and had to issue several maintenance releases in a row to address “showstopper” type bugs. Sadly the last of these was Tarrasch V3.03 *not* the aforementioned V3.02.

Oh well. I found it all a bit embarrassing at the time, and didn’t even make a blog post about V3.03. It turned out that V3.03 was the reliable workhorse that I hoped V3.00, then V3.01, then V3.02 would be. I am not the only one who suffers from this syndrome of course. I recall in the early days of my career Microsoft’s MS DOS V2.11 was “the golden one” that was the current and reliable version of their flagship operating system for a long long time (years if I remember correctly – or maybe time just went slower when I was a young man). They probably had great hopes for V2.10, V2.09 etc. as well.

Today I am not announcing a new Tarrasch version, although an updated version with some significant improvements shouldn’t be too much longer. (Spoiler alert: The biggest single change will be that the long awaited Linux native version is imminent).

I do have a small package to deliver though. There was really no excuse to have a more than year old version of Kingbase Lite for download, when Pierre Havard updates it regularly.  So I have updated the standalone Tarrasch database, available from the downloads page of triplehappy.com.

Just a quick note on how I build this database (as much as anything this will serve as a note to myself next time);

I download Pierre’s 2018 Kingbase Lite pgn and the monthly updates. I unzip everything, which gives me a mass of pgn files. I do a dir/b command from the Windows command line to get a list of the files in a text file and I wrangle that into an old fashioned DOS batch file that concatenates all the separate files into one big pgn. Just to be sure the concatenation works properly I add a crlf.txt file (a simple two character, one empty line text file) after each pgn file as I concatenate. This makes absolutely sure there’s a blank line between the last game in one file and the first game in the next (pgn files should end with a blank line – but this makes doubly sure).

For the masochistic here’s what my batch file looked like;

copy KingBaseLite2018-01.pgn + crlf.txt + KingBaseLite2018-02.pgn + crlf.txt + KingBaseLite2018-03.pgn + crlf.txt + KingBaseLite2018-04.pgn + crlf.txt + KingBaseLite2018-05.pgn u.pgn
copy KingBaseLite2018-A00-A39.pgn + crlf.txt + KingBaseLite2018-A40-A79.pgn + crlf.txt + KingBaseLite2018-A80-A99.pgn a.pgn
copy KingBaseLite2018-B00-B19.pgn + crlf.txt + KingBaseLite2018-B20-B49.pgn + crlf.txt + KingBaseLite2018-B50-B99.pgn b.pgn
copy KingBaseLite2018-C00-C19.pgn + crlf.txt + KingBaseLite2018-C20-C59.pgn + crlf.txt + KingBaseLite2018-C60-C99.pgn c.pgn
copy KingBaseLite2018-D00-D29.pgn + crlf.txt + KingBaseLite2018-D30-D69.pgn + crlf.txt + KingBaseLite2018-D70-D99.pgn d.pgn
copy KingBaseLite2018-E00-E19.pgn + crlf.txt + KingBaseLite2018-E20-E59.pgn + crlf.txt + KingBaseLite2018-E60-E99.pgn e.pgn
copy a.pgn + crlf.txt + b.pgn + crlf.txt + c.pgn + crlf.txt + d.pgn + crlf.txt + e.pgn + crlf.txt + u.pgn big.pgn

The final steps are a lot easier. I opened the resulting file, literally “big.pgn” in Tarrasch. I sort first on Round number then on Site, then on Date. The last sort is the most significant so I end up with most recent games first (sort on Date) with all games from an event together (sort on Site) and games from the same event on the same day ordered by round number / board (sort on Round). Then I save the file, now nicely sorted.

I am rather proud of the sorting facilities in Tarrasch, which absorbed an awful lot of effort in late 2016 early 2017!

Next I just create a database using this single file. Voila.

As a check I then copied the input files to my Ubuntu 16.04LTS Box and repeated the whole exercise (including wrangling the DOS batch file into a Bash shell script), and made sure that the resulting database not only worked beautifully on my Linux Tarrasch (it does) but that it also matches byte for byte with the database created on Windows (it does).

Sorry again I’ve gone a year without a blog post. If you really want to keep up with the minutiae of work on Tarrasch you can always go and look at the open source repository at Github.com/billforsternz. Check the development branch rather than the master branch (edited: 26 Nov 2018 – day to day work now in master branch not development branch), because that is where day to day work takes place.

 

Tarrasch V3.02a

I released Tarrasch V3.02a today. It is a maintenance (i.e. bugfix) release just like V3.01a three months ago. My apologies that releases like this are necessary.  Tarrasch V3 is now about 4 months old, and hopefully is becoming more refined as small (and not so small) problems are noticed and fixed. Here is the changelog for V3.02a

• Annoying problems with editing games with many variations and comments (so that the edit window needs to scroll) fixed. The edit cursor no longer jumps to bottom line, and scroll position is preserved if you switch tabs.
• A side effect of the fix above is that text editing (for comments) is faster than ever, faster than previous V3 versions and *much* faster than V2.
• Introduce Tarraschbase – Kingbase lite 2016-03 plus more recent games from Twic. This is hopefully a temporary measure until Kingbase is updated again.
• Screen adjustment for improved games dialog behaviour on commodity 720p laptops.
• Kibitz box is dynamically scaled to show all four lines – not always 99 pixels high.
• Deleting games in games dialogs behaves better.
• Stalemate and Checkmate positions no longer sent to engine for analysis.
• Bug fixed: (Bug was; Cannot save recalculated ECOs to file.)
• Bug fixed: (Bug was; Modify game -> make new tab -> go back to game -> undo changes game still shows as modified even though undo stack correctly shown as empty).
• Inappropriate sharing of pgn games dialog help screen with clipboard and session games dialogs corrected.
• Long overdue update from Komodo V3 to Komodo V8 (apologies for not noticing that the Komodo free version has changed dramatically).

I have put the most serious things first in this list. The top item was a very disappointing problem that I didn’t notice until I started doing some serious work with Tarrasch V3 (basically editing large games). It had the additional bad attribute that it was very hard to fix! I am very happy to see the back of it and I hope other users notice the improvement made.

Something else worth noticing is that the standard KingBase Lite database shipped with Tarrasch V3 was getting very stale, so I have added all the 2200 Elo plus games published on TWIC since the last update in March 2016. So a full year’s top level games. I feel a bit guilty about this, I was happy to have a third party collecting games instead. I hope Pierre Havard starts updating KingBase again soon. I’ve called the modified KingBase Lite  “Tarraschbase” for want of a better name. I really hope this is an interim measure. I plan on contacting Mark Crowther to tell him I am doing this, I suppose it’s possible he will ask me to stop. I’ll cross that bridge when I get to it.

 

Tarrasch V3.01a

I’ve been reasonably happy with the debut of Tarrasch V3. I’ve had about 10,000 downloads in the first month. Not too shabby. I must admit I was hoping that with V3 Tarrasch would make the jump from fringe player to first class citizen, but that hasn’t really happened yet. I’m not sure what it will take to elevate Tarrasch’s profile. Basically I will be happy if it is regularly mentioned as a valid alternative to Winboard, Arena and Scid. My own experience with those programs is that they can all do things Tarrasch can’t, but overall I much prefer Tarrasch as a general purpose chess workhorse. Of course it’s possible I am completely crazy. I am definitely completely biased!

Anyway, the real point of this post is to explain a new “bug fix” release of Tarrasch, V3.01a, available immediately from triplehappy.com.

I really wish this release wasn’t necessary, but sadly, almost inevitably, glitches and downright bugs show up. Here is my change log for V3.01a

• Add progress gauge when writing duplicate games, previously this slow operation appeared as stuck progress
• Title of progress bar during duplicate pgn file write allows discoverability
• Write duplicate pgn file after database written – so it is optional and can be cancelled
• Engine dialog box works on smaller screens
• Arrows allow tab navigation when number of tabs fills main screen
• Heading in frame is the default option
• Pattern search – “Don’t allow extra material” no longer the default!
• Avoid slowly leaking memory on meta-data as databases loaded or created
• Problems with pattern and material balance searches using clipboard as temporary database – fixed
• Ctrl-A = select all finally works in game dialogs
• Error handling in append database was broken – sometimes (eg unrecognised file format) leaving user unsure what happened
• Slightly more informative “can’t load database” message
• Never show asterisk = file modified if no current file!
• Order files after database append as intended – so most recent games appear first

I take comfort from the fact that none of these are “showstopper” type problems, despite frantic work and change right up to the last minute before V3 release. So my take is that V3.00a was a decent release and V3.01a is only a modest delta.

The development of Tarrasch V3 was complicated by the fact that I took several steps back, completely breaking Tarrasch V2, before I started moving forward again. So I always had two quite different versions; Stable but uninspiring V2 and fast moving but incomplete and broken V3. I’ll take this as a lesson and try and avoid doing something similar again. The idea now is that V3 is a stable platform that I can incrementally improve. The V3.01a release is the first example of this pattern in practice.

I am going to take a bit of a break now. There are many good ideas for Tarrasch enhancements that I just couldn’t quite fit in. In 2017 I hope to take another look and hopefully I will be able to incrementally improve Tarrasch with new and useful features.

 

Tarrasch V3 Released Successfully

As I described in a previous blog post, I finally released Tarrasch V3 on November 25th. Through some mechanism that remains a mystery to me, people noticed and download frequency went up immediately. Around a thousand downloads in the first day, over five thousand in total now after twelve days or so.

In the days following the release I developed a weird kind of anxiety I haven’t experienced with Tarrasch before. No doubt this was due to the release being the culmination of an awful lot of work. Tarrasch V3 is a tiny insignificant thing in the world – but for me it’s something of a big deal and if it turned out that I’d released prematurely and made some hideously embarrassing error it would have been bitterly disappointing. For several days I couldn’t bear to even run my own program – I was too worried it would just crash hopelessly in some trivial way due to an obvious use case I’d somehow neglected.

Happily I got over than after a few days, and started poking around and even stretching my program a little again. The dreaded deluge of angry emails I was imagining didn’t materialise, and instead I got a trickle :- (not a deluge unfortunately), of nice feedback instead.

The title of this post is “Tarrasch V3 Released Successfully” and basically this means that Tarrasch V3 has finally replaced Tarrasch V2, and as far as I can tell the transition has been a smooth one.

This is not to say that there are no problems – but I think the ones that have come to my attention so far at least are of the kind that you can reasonably expect. I will issue a .01 update in due course and life will go on. At this point here are the issues I feel I need to fix fairly promptly;

• At the end of a big database create or append operation, writing out a large number of discarded duplicate games to the discarded duplicates .pgn takes a long time and this delay is not predicted or acknowledged by the progress indicator (the user might wrongly perceive that the program has crashed).
• If there are more tabs than can be comfortably accommodated – the most recent tabs aren’t selectable until older tabs are deleted to make room.
• If the vertical resolution is less than 766 pixels, the option engine dialog doesn’t let the user change engines.
• I think I was wrong to move the position heading (“Position after 1.e4” etc) from the frame to the board pane by default. On all but very large screens it takes too much room.